一、关键路径的定义

　　拓扑排序主要为了解决一个工程能否顺序进行的问题，但有时候还需要解决工程完成需要的最短时间问题。

　　1.AOE网：在一个表示工程的带权有向图中，用顶点表示时间，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，称为AOE网（Activity On Edge Network）。把AOE网中没有入边的顶点称为始点或源点，没有出边的顶点称为终点或汇点。正常情况下，AOE网只有一个源点一个汇点。

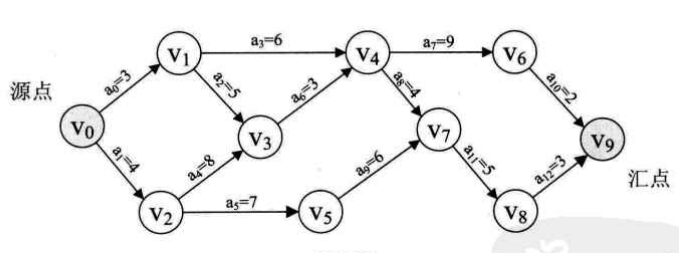　　弧<v0，v1>表示从源点开始的第一个活动a0，它的时间单位是3个单位。

　　2.关键路径：把路径上各个活动所持续时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。

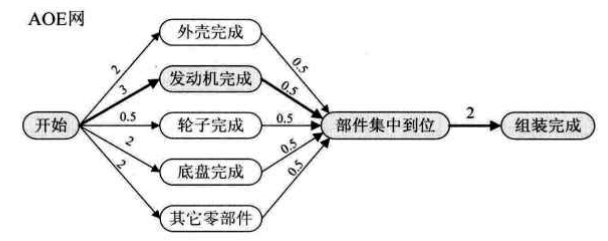　　关键路径为：开始-发动机完成-部件集中到位-组装完成。路径长度为3+0.5+2=5.5小时

 

　　二、关键路径算法

　　1.为了找到所有活动的最早开始时间和最晚开始时间，并且比较它们，如果相等就意味着此活动是关键活动，活动间的路径为关键路径。因此需要定义几个参数：

• 事件的最早发生时间etv(earliest time of vertex)：即顶点Vk的最早发生时间。
• 事件的最晚发生时间ltv(lastest time of vertex)：即顶点Vk的最晚发生时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个工期。
• 活动的最早开工时间ete(earliest time of edge)：即弧Ak的最早发生时间。
• 活动的最晚开工时间lte(lastest time of edge)：即弧Ak的最晚发生时间，也就是不推迟工期的最晚开工时间。

　　由etv和ltv可以求得ete和lte，然后再根据ete和lte是否相等来判断ak是否是关键活动。

　　2.关键路径算法的思路

　　假设V0为源点，时间V0发生的时刻为0时刻，从V0到Vi的最长路径叫做事件Vi的最早发生时间，这个时间决定以所有以Vi为尾的弧所表示活动的最早开始时间。用etv(i)表示活动ai的最早开始时间。还可以定义一个活动ai的最晚开始时间ltv(i)，这是在不推迟整个工程完成的前提下，活动ai最迟必须开始的时间。两者之差意味着完成活动ai的时间余量。当etv(i)=ltv(i)时的活动成为关键活动。由于关键路径上的活动都是关键活动，所以，提前完成非关键活动并不能加快工程的进度。

　　

　　例如，上图所示的AOE网的关键路径为：v0->v2->v3->v4->v7->v8->v9

　　因为事件a5的最早开始时间为4，而v0-v2-v3-v7的总时间为4+8+3+7=22，所以时间a5的最晚开始时间为22-4-6-7=5，即若a5延迟1小时，不会影响整个工程的完成。所以说a5不是关键活动。

　　3.关键路径算法C语言代码实现

#include "stdio.h"    #include "stdlib.h"   #include "io.h"  #include "math.h"  #include "time.h"#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAXEDGE 30#define MAXVEX 30#define INFINITY 65535typedef int Status;    /* Status是函数的类型,其值是函数结果状态代码，如OK等 */  int *etv,*ltv; /* 事件最早发生时间和最迟发生时间数组，全局变量 */int *stack2;   /* 用于存储拓扑序列的栈 */int top2;       /* 用于stack2的指针 *//* 邻接矩阵结构 */typedef struct{    int vexs[MAXVEX];    int arc[MAXVEX][MAXVEX];    int numVertexes, numEdges;}MGraph;/* 邻接表结构****************** */typedef struct EdgeNode /* 边表结点  */{    int adjvex;    /* 邻接点域，存储该顶点对应的下标 */    int weight;        /* 用于存储权值，对于非网图可以不需要 */    struct EdgeNode *next; /* 链域，指向下一个邻接点 */}EdgeNode;typedef struct VertexNode /* 顶点表结点 */{    int in;    /* 顶点入度 */    int data; /* 顶点域，存储顶点信息 */    EdgeNode *firstedge;/* 边表头指针 */}VertexNode, AdjList[MAXVEX];typedef struct{    AdjList adjList;     int numVertexes,numEdges; /* 图中当前顶点数和边数 */}graphAdjList,*GraphAdjList;/* **************************** */void CreateMGraph(MGraph *G)/* 构件图 */{    int i, j;    /* printf("请输入边数和顶点数:"); */    G->numEdges=13;    G->numVertexes=10;    for (i = 0; i < G->numVertexes; i++)/* 初始化图 */    {        G->vexs[i]=i;    }    for (i = 0; i < G->numVertexes; i++)/* 初始化图 */    {        for ( j = 0; j < G->numVertexes; j++)        {            if (i==j)                G->arc[i][j]=0;            else                G->arc[i][j]=INFINITY;        }    }    G->arc[0][1]=3;    G->arc[0][2]=4;     G->arc[1][3]=5;     G->arc[1][4]=6;     G->arc[2][3]=8;     G->arc[2][5]=7;     G->arc[3][4]=3;    G->arc[4][6]=9;     G->arc[4][7]=4;    G->arc[5][7]=6;     G->arc[6][9]=2;    G->arc[7][8]=5;    G->arc[8][9]=3;}/* 利用邻接矩阵构建邻接表 */void CreateALGraph(MGraph G,GraphAdjList *GL){    int i,j;    EdgeNode *e;    *GL = (GraphAdjList)malloc(sizeof(graphAdjList));    (*GL)->numVertexes=G.numVertexes;    (*GL)->numEdges=G.numEdges;    for(i= 0;i 
      
       adjList[i].in=0;        (*GL)->adjList[i].data=G.vexs[i];        (*GL)->adjList[i].firstedge=NULL;     /* 将边表置为空表 */    }        for(i=0;i
       
        adjvex=j;                    /* 邻接序号为j */                   e->weight=G.arc[i][j];                e->next=(*GL)->adjList[i].firstedge;    /* 将当前顶点上的指向的结点指针赋值给e */                (*GL)->adjList[i].firstedge=e;        /* 将当前顶点的指针指向e  */                  (*GL)->adjList[j].in++;                            }        }    }    }/* 拓扑排序 */Status TopologicalSort(GraphAdjList GL){    /* 若GL无回路，则输出拓扑排序序列并返回1，若有回路返回0。 */        EdgeNode *e;        int i,k,gettop;       int top=0;  /* 用于栈指针下标  */    int count=0;/* 用于统计输出顶点的个数 */       int *stack;    /* 建栈将入度为0的顶点入栈  */       stack=(int *)malloc(GL->numVertexes * sizeof(int) );        for(i = 0; i
        
         numVertexes; i++)                        if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */                       stack[++top]=i;        top2=0;        etv=(int *)malloc(GL->numVertexes * sizeof(int) ); /* 事件最早发生时间数组 */        for(i=0; i
         
          numVertexes; i++)                etv[i]=0;    /* 初始化 */    stack2=(int *)malloc(GL->numVertexes * sizeof(int) );/* 初始化拓扑序列栈 */    printf("TopologicalSort:\t");    while(top!=0)        {                gettop=stack[top--];                printf("%d -> ",GL->adjList[gettop].data);                count++;        /* 输出i号顶点，并计数 */         stack2[++top2]=gettop;        /* 将弹出的顶点序号压入拓扑序列的栈 */        for(e = GL->adjList[gettop].firstedge; e; e = e->next)                {                        k=e->adjvex;                        if( !(--GL->adjList[k].in) )        /* 将i号顶点的邻接点的入度减1，如果减1后为0，则入栈 */                                stack[++top]=k;             if((etv[gettop] + e->weight)>etv[k])    /* 求各顶点事件的最早发生时间etv值 */                                etv[k] = etv[gettop] + e->weight;        }        }        printf("\n");       if(count < GL->numVertexes)                return ERROR;        else               return OK;}/* 求关键路径,GL为有向网，输出G的各项关键活动 */void CriticalPath(GraphAdjList GL) {        EdgeNode *e;        int i,gettop,k,j;        int ete,lte;  /* 声明活动最早发生时间和最迟发生时间变量 */            TopologicalSort(GL);   /* 求拓扑序列，计算数组etv和stack2的值 */     ltv=(int *)malloc(GL->numVertexes*sizeof(int));/* 事件最早发生时间数组 */       for(i=0; i
          
           numVertexes; i++)                ltv[i]=etv[GL->numVertexes-1];    /* 初始化 */                printf("etv:\t");       for(i=0; i
           
            numVertexes; i++) printf("%d -> ",etv[i]); printf("\n"); while(top2!=0) /* 出栈是求ltv */ { gettop=stack2[top2--]; for(e = GL->adjList[gettop].firstedge; e; e = e->next) /* 求各顶点事件的最迟发生时间ltv值 */ { k=e->adjvex; if(ltv[k] - e->weight < ltv[gettop]) ltv[gettop] = ltv[k] - e->weight; } } printf("ltv:\t"); for(i=0; i
            
             numVertexes; i++) printf("%d -> ",ltv[i]); printf("\n"); for(j=0; j
             
              numVertexes; j++) /* 求ete,lte和关键活动 */ { for(e = GL->adjList[j].firstedge; e; e = e->next) { k=e->adjvex; ete = etv[j]; /* 活动最早发生时间 */ lte = ltv[k] - e->weight; /* 活动最迟发生时间 */ if(ete == lte) /* 两者相等即在关键路径上 */ printf("
              
                length: %d \n",GL->adjList[j].data,GL->adjList[k].data,e->weight); } }}int main(void){ MGraph G; GraphAdjList GL; CreateMGraph(&G); CreateALGraph(G,&GL); CriticalPath(GL); return 0;}
              
             
            
           
          
         
        
       
      

　　4.关键路径算法Java语言代码实现

　　（1）和拓扑排序时邻接表的边结点结构不同的是，关键路径算法时要用到每个边上时间ak的时间，因此需要在边结点结构中增加一个weight域来表示事件需要的时间。

package bigjun.iplab.criticalPath;/** * 用于关键路径算法中的邻接表存储结构中的边(或弧)结点类 */public class EdgeNode {    public int adjVex;                // 该弧所指向的顶点在顶点数组中的下标    public int weight;                // 用于表示事件完成需要的时间    public EdgeNode nextEdge;        // 指向下一条表示边或弧的结点类            public EdgeNode(int adjVex, int weight) {        this(adjVex, weight, null);    }        public EdgeNode(int adjVex, int weight, EdgeNode nextEdge) {        this.adjVex = adjVex;        this.weight = weight;        this.nextEdge = nextEdge;    }    }

　　（2）实现类：

package bigjun.iplab.criticalPath;import bigjun.iplab.linkStack.LinkStack;public class TheCriticalPath {    private static LinkStack T = new LinkStack();        // 拓扑逆序列顶点栈    private static int[] etv, ltv;                        // 各顶点的最早发生时间和最晚发生时间        public static void CriticalPath(ActivityOnEdgeNetwork G) throws Exception {                if (!topologicalOrder(G))             throw new Exception("给定的AOE网是一个带回环的网图，不能找到关键路径！");        ltv = new int[G.getVexNum()];        for (int i = 0; i < G.getVexNum(); i++) {            ltv[i] = etv[G.getVexNum() - 1];        }        while (!T.isStackEmpty()) {            int i = (int) T.stackPop();            for (EdgeNode edge = G.getVexs()[i].firstEdge; edge != null; edge = edge.nextEdge) {                int k = edge.adjVex;                int time = edge.weight;                if (ltv[k] - time < ltv[i])                     ltv[i] = ltv[k] - time;            }        }                for (int i = 0; i < G.getVexNum(); i++) {            for (EdgeNode edge = G.getVexs()[i].firstEdge; edge != null; edge = edge.nextEdge) {                int k = edge.adjVex;                int time = edge.weight;                int ete = etv[i];                int lte = ltv[k] - time;                char tag = (ete==lte)? 'Y':'N';                System.out.println(G.getVex(i) + "->" + G.getVex(k) + " " + "活动持续的时间: " + time + " "                 + "最早开始时刻: " + ete + " " +  "最晚开始时刻: "+ lte + " " + "是否是关键路径 : " + tag);            }        }    }        // 使用拓扑排序求事件的最早发生时间etv，以及将拓扑序列存入全局变量栈T中    private static boolean topologicalOrder(ActivityOnEdgeNetwork G) throws Exception {        int count = 0;                                  // 统计输出顶点的个数        LinkStack S = new LinkStack();                for (int i = 0; i < G.getVexNum(); i++) {        // 将入度为0的顶点入栈            if (G.getVexs()[i].in == 0) {                S.stackPush(i);            }        }        etv = new int[G.getVexNum()];        while (!S.isStackEmpty()) {            int i = (int) S.stackPop();            T.stackPush(i);            count++;            // 遍历顶点Vi的边链表，将每一个弧头对应的顶点的入度减1，也就是把Vi和连接自己的弧断开            for (EdgeNode edge = G.getVexs()[i].firstEdge; edge != null; edge = edge.nextEdge) {                int k = edge.adjVex;                if (--G.vexs[k].in == 0) {                    S.stackPush(k);                }                if (etv[i] + edge.weight > etv[k])                     etv[k] = etv[i] + edge.weight;            }        }        if (count < G.getVexNum())             return false;            // 如果遍历完后count值小于总的顶点数，就说明该有向图有回路，即拓扑排序的过程中又绕回去了        else             return true;                }    }

　　（3）测试代码（以下面的AOE网为例）：

　　

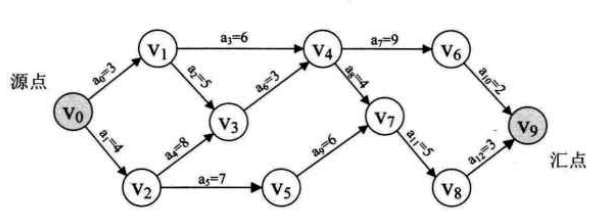
public static ActivityOnEdgeNetwork createDN_ForTheCriticalPath() {                EdgeNode e_0_1 = new EdgeNode(1, 3);        EdgeNode e_0_2 = new EdgeNode(2, 4, e_0_1);        VertexNode v0 = new VertexNode(0, "V0", e_0_2);                EdgeNode e_1_3 = new EdgeNode(3, 5);        EdgeNode e_1_4 = new EdgeNode(4, 6, e_1_3);        VertexNode v1 = new VertexNode(1, "V1", e_1_4);                EdgeNode e_2_3 = new EdgeNode(3, 8);        EdgeNode e_2_5 = new EdgeNode(5, 7, e_2_3);        VertexNode v2 = new VertexNode(1, "V2", e_2_5);                EdgeNode e_3_4 = new EdgeNode(4, 3);        VertexNode v3 = new VertexNode(2, "V3", e_3_4);                EdgeNode e_4_6 = new EdgeNode(6, 9);        EdgeNode e_4_7 = new EdgeNode(7, 4, e_4_6);        VertexNode v4 = new VertexNode(2, "V4", e_4_7);                EdgeNode e_5_7 = new EdgeNode(7, 6);        VertexNode v5 = new VertexNode(1, "V5", e_5_7);                EdgeNode e_6_9 = new EdgeNode(9, 2);        VertexNode v6 = new VertexNode(1, "V6", e_6_9);                EdgeNode e_7_8 = new EdgeNode(8, 5);        VertexNode v7 = new VertexNode(2, "V7", e_7_8);                EdgeNode e_8_9 = new EdgeNode(9, 3);        VertexNode v8 = new VertexNode(1, "V8", e_8_9);                VertexNode v9 = new VertexNode(2, "V9");                VertexNode[] vexs = {v0,v1,v2,v3,v4,v5,v6,v7,v8,v9};                int vertexNum = vexs.length;        int edgeNum = 13;                return new ActivityOnEdgeNetwork(vertexNum, edgeNum, vexs);            }        public static void main(String[] args) throws Exception {        ActivityOnEdgeNetwork DN_ForCriticalPath = createDN_ForTheCriticalPath();        TheCriticalPath.CriticalPath(DN_ForCriticalPath);    }

　　（4）输出

V0->V2 活动持续的时间: 4 最早开始时刻: 0 最晚开始时刻: 0 是否是关键路径 : YV0->V1 活动持续的时间: 3 最早开始时刻: 0 最晚开始时刻: 4 是否是关键路径 : NV1->V4 活动持续的时间: 6 最早开始时刻: 3 最晚开始时刻: 9 是否是关键路径 : NV1->V3 活动持续的时间: 5 最早开始时刻: 3 最晚开始时刻: 7 是否是关键路径 : NV2->V5 活动持续的时间: 7 最早开始时刻: 4 最晚开始时刻: 6 是否是关键路径 : NV2->V3 活动持续的时间: 8 最早开始时刻: 4 最晚开始时刻: 4 是否是关键路径 : YV3->V4 活动持续的时间: 3 最早开始时刻: 12 最晚开始时刻: 12 是否是关键路径 : YV4->V7 活动持续的时间: 4 最早开始时刻: 15 最晚开始时刻: 15 是否是关键路径 : YV4->V6 活动持续的时间: 9 最早开始时刻: 15 最晚开始时刻: 16 是否是关键路径 : NV5->V7 活动持续的时间: 6 最早开始时刻: 11 最晚开始时刻: 13 是否是关键路径 : NV6->V9 活动持续的时间: 2 最早开始时刻: 24 最晚开始时刻: 25 是否是关键路径 : NV7->V8 活动持续的时间: 5 最早开始时刻: 19 最晚开始时刻: 19 是否是关键路径 : YV8->V9 活动持续的时间: 3 最早开始时刻: 24 最晚开始时刻: 24 是否是关键路径 : Y

　　（5）以实例分析代码执行过程

　　

初始化，入度为0的顶点v0入栈S， 栈S不为空，将顶点v0从S中出栈，i=0，将0入栈到T中，count=1，进入for循环，k=2，v2的入度减1到0，v2入栈S，etv[2]+e02的权值4=4，etv[2]=0,etv[2]=4,即顶点v2最早发生时刻为4 栈S不为空，将顶点v2从S中出栈，i=2，将2入栈到T中，count=2，进入for循环，k=5，v5的入度减1到0，v5入栈S，etv[2]+e25=4+7=11,etv[5]=0,则etv[5]=11， ...同理，要求etv[3]的话，也就是v3最早发生时刻，只要比较etv[1]+a2和etv[2]+a4这两个中哪个大就行了，因为etv[1]和etv[2]分别是v0到v1和v2的最早时刻。从而etv[3]=13 最后得到etv[]={0,3,4,12,15,11,25,19,24,27}即各个顶点的最早发生时刻，T中：（top）9 8 7 5 6 4 3 2 1 0是拓扑排序的逆序 然后进入关键路径主函数：初始化ltv[]={27,27,27,27,27,27,27,27,27,27}即为etv中的最大值 -T不为空，9出栈i=9，没有邻接表，跳出 -T不为空，8出栈i=8，k=9，time=3，ltv[9]-3=27-3=24,ltv[8]=27,则ltv[8]=24,即v8的最晚发生时刻是24 -T不为空，7出栈i=7，k=8，time=5，ltv[8]-5=24-5=19,ltv[7]=27,则ltv[7]=19,即v7的最晚发生时刻是19 -T不为空，5出栈i=5，k=7，time=6，ltv[7]-6=19-6=13,ltv[5]=27,则ltv[5]=13,即v5的最晚发生时刻是13 -T不为空，6出栈i=6，k=9，time=2，ltv[9]-2=27-2=15,ltv[6]=27,则ltv[6]=25,即v8的最晚发生时刻是25 此时，ltv[] ={27,27,27,27,27,13,25,19,24,27} -T不为空，4出栈i=4，k=7，time=4，ltv[7]-4=19-4=15,ltv[4]=27,则ltv[4]=15,则v4的最晚发生时刻是 　　　　　　　　　　 k=6，time=9，ltv[6]-9=25-9=16,ltv[4]=15,则ltv[4]仍然等于15，则v4的最晚发生时刻是15 这里可以很清楚的看到，由于v6最晚开始时刻是25，而v7最晚开始时刻是19，所以v4走v6和v7的时候最晚发生时刻分别为：15,16所以v4最晚都要在15时刻开始发生， 如果16才发生的话，就到v7晚了， 所以说ltv[k]=min{ltv[j] - len
     
      ,其中j就是以vk为弧尾的弧的弧头顶点下标} 最后得到 etv[]={0,3,4,12,15,11,25,19,24,27} ltv[]={0,7,4,12,15,13,25,19,24,27}可以看到v1表示的事件即使在7时刻才发生，也不会影响整个工程的进度。 ete表示
      
       活动的最早开工时间，也就是只有vi事件发生了，活动才可以开始，因此ete=etv[i] 而lte表示
       
        的最晚开工时间，但此活动再晚也不能等待vk事件发生了才发生，所以必须要在vk事件发生前发生，所以lte=ltv[k]-len
        
          最后，通过比较ete和lte来判断弧
         
          对应的路径是不是关键路径。